Cỡ mẫu cho các nghiên cứu mô tả trong y học

Một trong những quyết định khó khăn nhất mà nhà nghiên cứu phải đối mặt là mẫu phải lớn như thế nào. Hai cách tiếp cận phổ biến được sử dụng trong các nghiên cứu: thực nghiệm và phân tích. Phương pháp thực nghiệm liên quan đến việc sử dụng các cỡ mẫu đã được sử dụng trong các nghiên cứu tương tự. Điều này không có cơ sở khoa học và sẽ chỉ thỏa đáng nếu các nghiên cứu trước đây có giới hạn chấp nhận được về sai số tổng quát và nghiên cứu hiện tại rất giống nhau về phạm vi (mục tiêu, thiết kế, quần thể nghiên cứu, v.v.). Phương pháp này không được khuyến khích và sẽ không được thảo luận thêm.

Cách tiếp cận phân tích (khoa học) để xác định kích thước thích hợp của mẫu được đưa vào nghiên cứu phụ thuộc vào việc đánh giá sai số của suy luận và mong muốn giảm thiểu "sai số lấy mẫu". Sai số lấy mẫu đo lường mức độ thay đổi giữa các kết quả mẫu (như một đại diện cho sự gần gũi với tình hình thực tế trong tổng thể và được tái hiện trong kết quả mẫu); kết quả mẫu càng ít biến đổi thì kết quả mẫu càng gần với kết quả tổng thể.

Do đó, yếu tố quyết định chính của cỡ mẫu là kết quả cần phải chính xác đến mức nào. Điều này phụ thuộc vào mục đích của nghiên cứu (nghiên cứu mô tả để xác định thước đo tóm tắt của một đặc tính, hoặc nghiên cứu phân tích trong đó các bộ giả thuyết cụ thể đang được kiểm tra).

Trong trường hợp nghiên cứu mô tả, thường mục tiêu là thu được ước tính của một tham số quần thể. Ví dụ, trong các cuộc thăm dò dư luận, nhà nghiên cứu thị trường có thể quan tâm đến việc tìm ra tỷ lệ người dân thích một thương hiệu cụ thể nào. Một chuyên gia dinh dưỡng có thể quan tâm đến lượng calo trung bình hàng ngày của quần thể Một nhà nghiên cứu sức khỏe có thể quan tâm đến tỷ lệ người hút thuốc, hoặc tỷ lệ sống sót trung bình sau phẫu thuật bắc cầu mạch vành. Việc xác định cỡ mẫu cần thiết để trả lời những câu hỏi này phụ thuộc vào một số yếu tố:

1). Mức độ quan tâm? Điều này sẽ được xác định bởi các mục tiêu nghiên cứu. Việc xác định đặc trưng của tầm quan trọng chính xác định các bước tiếp theo trong quá trình xác định cỡ mẫu. Ví dụ, nếu một tỷ lệ hiện mắc trong dân số được ước tính bằng cách quan sát một mẫu từ quần thể, thì số đo là tỷ lệ người trong mẫu mắc bệnh.

2). Phân phối xác suất cơ bản của đặc tính quan tâm? Hầu hết các câu hỏi nghiên cứu rơi vào một trong hai trường hợp có thể xảy ra: phân phối nhị thức (khi người ta muốn ước tính tỷ lệ của một sự kiện nhất định) và phân phối chuẩn (khi người ta muốn ước tính giá trị trung bình). Ví dụ, nhà nghiên cứu thị trường ở trên coi sự ưa thích của một thương hiệu là đặc điểm, với hai kết quả có thể xảy ra. Nếu người ta giả định rằng có thể có một tỷ lệ (π) cố định của những người ưa thích nhãn hiệu, thì số người bày tỏ sở thích này trong bất kỳ nhóm người cố định nào sẽ tuân theo phân phối nhị thức, với tỷ lệ (p) của những người cho thấy mức độ ưa thích như một ước tính tốt về tỷ lệ dân số. Đối với chuyên gia dinh dưỡng, lượng calo hàng ngày của các cá nhân tuân theo phân phối chuẩn với một số trung bình (µ), và mức trung bình của lượng calo hàng ngày của mẫu người (x) được quan sát sẽ là một ước tính tốt về giá trị quần thể này.

3). Phân bố lấy mẫu của thước đo? Việc rút ra các suy luận từ mẫu đến tổng thể bao gồm các sai số cố hữu, được đo bằng phân bố lấy mẫu. Nếu chúng tôi quan sát một số mẫu, trong cùng một phương pháp chọn mẫu, các số đo từ mỗi mẫu này sẽ khác nhau, dẫn đến 'phân phối xác suất' cho phép đo mẫu. Phân bố này được gọi là phân bố lấy mẫu, và nó phụ thuộc vào kiểu thiết kế nghiên cứu và cách lấy mẫu. Khi tính toán cỡ mẫu, người ta thường giả định rằng việc lấy mẫu bao gồm lấy mẫu ngẫu nhiên đơn giản. Đôi khi thiết kế lấy mẫu phức tạp hơn nhiều (ví dụ: kỹ thuật lấy mẫu cụm nhiều tầng) và các công thức phức tạp hơn sẽ phải được sử dụng để tính toán cỡ mẫu một cách thích hợp.

4). Kết quả chính xác đến mức nào? Về cơ bản, người ta quan tâm đến việc có được một ước tính càng gần với giá trị quần thể càng tốt. Do đó, một số thước đo của sự khác biệt giữa ước tính và giá trị dân số phải được xem xét. Trong hầu hết các trường hợp, sai số trung bình bình phương (trung bình của độ lệch bình phương của giá trị mẫu so với giá trị tổng thể) được sử dụng. Một cách ngắn gọn để diễn đạt sai số này là sử dụng 'sai số tiêu chuẩn của ước tính'. Sai số tiêu chuẩn đến từ sự phân phối lấy mẫu của ước lượng. Nếu việc lấy mẫu được thực hiện đúng cách (với các phương pháp xác suất thích hợp), người ta có thể dự đoán phân bố này nên là bao nhiêu, và dựa trên điều này, người ta có thể ước tính mức độ gần với giá trị dân số mà ước tính mẫu sẽ là:

Ví dụ, trong trường hợp ước tính tỷ lệ quần thể, phân bố lấy mẫu của tỷ lệ mẫu, p là xấp xỉ bình thường, với giá trị trung bình là π và phương sai π (1-π) / n, trong đó n là cỡ mẫu. Điều này cho ta khoảng tin cậy (1-α) cho π là:

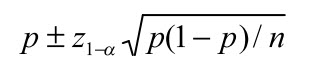
trong đó z _1-α   là điểm cắt thích hợp trên phân phối chuẩn chuẩn. (Ví dụ: với độ tin cậy 95%, z _1-α   = 1,96).

Do đó, độ chính xác của ước tính phụ thuộc vào hai đại lượng: khoảng này hẹp như thế nào (chiều rộng của khoảng) và mức độ tin cậy của chúng ta (ví dụ: 95%).

Do đó, việc tính toán kích thước của mẫu cho một nghiên cứu mô tả phụ thuộc vào hai tham số - độ rộng của khoảng tin cậy và hệ số tin cậy. Các chương trình máy tính luôn có sẵn. Hai kịch bản phổ biến, ước tính tỷ lệ dân số và ước tính trung bình dân số, được minh họa dưới đây:

1). Ước tính tỷ lệ dân số (p). Giả sử chúng ta muốn thực hiện một cuộc khảo sát để xác định tỷ lệ hiện mắc (π) của một bệnh tương đối phổ biến trong một cộng đồng. Chúng tôi muốn xác định có bao nhiêu người nên được quan sát để có được bức tranh chính xác hợp lý về tỷ lệ hiện mắc. Các bước sau là cần thiết:

Chỉ định các tham số của lỗi:

Hệ số tin cậy (1-α): 95%

Chiều rộng của khoảng (δ): 10%

Dự đoán giá trị của π: 30%

Vấn đề là tính toán cỡ mẫu cần thiết để ước tính tỷ lệ hiện mắc bệnh trong khoảng ± 5% giá trị thực, với độ tin cậy 95%. Vì khoảng tin cậy thực sự phụ thuộc vào giá trị thực, p, nên chúng ta phải đoán xem giá trị này có thể là bao nhiêu. Điều này được thực hiện dựa trên kinh nghiệm trước đó; nếu không có sẵn phỏng đoán, hãy sử dụng giá trị 50%, giá trị này sẽ cung cấp kích thước mẫu lớn nhất. Sử dụng thực tế rằng tỷ lệ mẫu (p) có khoảng tin cậy đã cho ở trên, cỡ mẫu (n) có thể được tính bằng công thức:

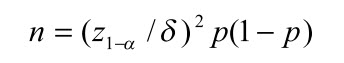
Do đó, trong ví dụ trên, n = (1,96 / 5) 2 (30 * 70) = 323; chúng ta cần tối thiểu 323 đối tượng được quan sát để đảm bảo rằng khoảng tin cậy 95% cho tỷ lệ ước tính sẽ nằm trong 5% tỷ lệ phổ biến thực sự. Nếu tỷ lệ phổ biến thực sự nhỏ hơn 30%, khoảng tin cậy sẽ hẹp hơn. Kích thước mẫu tối đa được yêu cầu sẽ xảy ra khi tỷ lệ phổ biến thực sự là 50%, trong trường hợp đó, n = 385.

Tính toán trên giả định một mẫu ngẫu nhiên đơn giản từ một tập hợp tương đối lớn. Trong thực tế, quần thể mà từ đó các mẫu được lấy ra có thể cố định và nhỏ, trong trường hợp đó, cần phải điều chỉnh các công thức trên.

2). Ước tính trung bình quần thể (µ). Giả sử chúng ta muốn ước tính lượng calo trung bình hàng ngày của mọi người trong một cộng đồng. Lượng calo hàng ngày được giả định có phân phối chuẩn xung quanh µ, với độ lệch chuẩn (σ).

Số đo mẫu được sử dụng để ước tính µ là giá trị trung bình của mẫu.

Phân bố lấy mẫu của trung bình mẫu cũng chuẩn, với cùng giá trị trung bình, µ và độ lệch chuẩn, σ / √n (sai số chuẩn của giá trị trung bình). Chú ý rằng chúng ta cần biết giá trị của σ để tiếp tục. Nó có thể thu được từ các nghiên cứu tương tự khác, hoặc thực sự thu được một số lượng nhỏ các quan sát ngẫu nhiên trong một nghiên cứu thử nghiệm. Nếu cả hai điều này đều không khả thi, người ta có thể đưa ra một dự đoán hợp lý bằng cách lấy phạm vi lớn nhất (giá trị lớn nhất có thể - giá trị nhỏ nhất có thể) và chia phạm vi này cho 4. (Sử dụng giả thiết rằng đối với phân phối chuẩn, 95% giá trị sẽ nằm trong ± 2 độ lệch chuẩn so với giá trị trung bình và giá trị trung bình sẽ là giá trị trung tâm.) Sau đó, các bước sau sẽ giúp tính toán kích thước mẫu:

Chỉ định các thông số lỗi:

Hệ số tin cậy (1-α): 95%

Chiều rộng của khoảng (δ): 50 cal.

Độ lệch chuẩn (σ): 150 cal.

Khoảng tin cậy 95% cho giá trị trung bình của mẫu là:

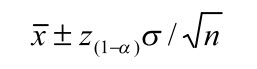
Do đó, kích thước mẫu bắt buộc trong ví dụ là:

n = (1,96 * 150/50)² = 35.

3). Ước tính rủi ro tương đối hoặc tỷ lệ chênh lệch. Các công thức để tính toán cỡ mẫu trong những tình huống này phức tạp hơn nhiều, vì việc lấy mẫu phân phối các ước tính về rủi ro tương đối và tỷ lệ chênh lệch không đơn giản. Các chương trình máy tính khác nhau có sẵn để tính toán kích thước mẫu thích hợp.

Về cơ bản, các nguyên tắc giống nhau: xác định công thức cho khoảng tin cậy và bằng cách chỉ định hai tham số, hãy tính cỡ mẫu từ công thức này.